通信原理实验二

实验报告

实验目的

1.加深理解DSB-SC、AM、SSB三种调幅方法的调制和解调原理及实现方法；
2.通过实验观察信号的功率谱；
3.在信道中加入噪声，观察对输出信号的影响。

实验原理

1.双边带抑制载波调幅（DSB-SC）设均值为零的模拟基带信号为m(t)，双边带抑制载波调幅（DSB-SC）信号为$s(t)=m(t)cos2 \pi f_ct$ , 当m(t)是随机信号，其功率谱密度为$P_s(f)=\frac{1}{4}[P_M(f-f_c)+P_M(f+f_c)]$,当m(t)是确知信号，其频谱为$S(f)=\frac{1}{2}[M(f-f_c)+M(f+f_c)]$,其中$P_M(f)$是m(t)的功率谱密度，M(t)是m(t)的频谱。由于m(t)均值为0，因此调制后的信号不含离散的载波分量，若接收端能恢复出载波分量，则可以采用如下的相干解调$r(t)=s(t)cos2 \pi f_ct=m(t)cos^{2}2 \pi f_ct= \frac{1}{2}m(t)+ \frac{1}{2}m(t)cos4 \pi f_ct$,再用低通滤波器滤去高频分量，就恢复出了原始信息。
2.具有离散大载波的双边带调幅（AM）设模拟基带信号为m(t)，调幅信号为$s(t)=[A+m(t)]cos2 \pi f_ct$，其中A是一个常数。可以将调幅信号看成一个余弦载波加抑制载波双边带调幅信号，当A>m(t)时，称此调幅信号欠调幅；A<m(t)时，为过调幅。当m(t)的频宽远小于载波频率时，欠调幅信号可以用包络检波的方式解调，而过调幅信号只能通过相干解调。
3.单边带调幅（SSB）模拟基带信号m(t)经过双边带调制后，频谱被搬移到中心频率为$\pm f_c$，但从恢复原信号频谱的角度看，只要传输双边带信号的一半带宽就可以完全恢复出原信号的频谱。因此，单边带上边带信号可以表示成$s(t)= \frac{1}{2}m(t)cos2 \pi f_ct- \frac{1}{2} \overbrace{m} (t)sin2 \pi f_ct$,同理，单边带下边带信号可表示为$s(t)= \frac{1}{2}m(t)cos2 \pi f_ct- \frac{1}{2} \overbrace{m} (t)sin2 \pi f_ct$。在接收端，可以通过相干解调方式对单边带信号进行解调。

实验内容

用Matlab产生一个频率为1Hz、功率为1的余弦信源，设载波频率为10Hz，试画出：
1.DSB调制信号及其功率谱密度；

clc,clear,close all;
dt=0.001; 
t=-10:dt:10; % 仿真时间
fm=1;%基带信号频率 
fc=10;%载波频率
mt=sqrt(2)*cos(2*pi*fm*t);%基带信号
c=cos(2*pi*fc*t);%载波信号
st=mt.*c;%DSB
%求功率谱
T=20;
df=1/T;% 抽样精度
N=length(st);%确定抽样个数
f=-N/2*df:df:N/2*df-df;%功率谱范围
sf=fft(st);%傅里叶变化
sf=T/N*fftshift(sf);%将零频点移到频谱的中间
psf=(abs(sf).^2)/T;%求功率
%绘制基带信号
subplot(311)
plot(t,mt)
xlabel('t');
ylabel('mt');
%plot(t,mt,'r--')
title('基带信号波形');
axis([-5,5,-1.5,1.5]);
grid on;
%绘制DSB波形
subplot(312)
plot(t,st)
xlabel('t');
ylabel('st');
hold on;
plot(t,mt,'r--');
title('DSB调制波形');
legend('DSB','基带信号')
axis([-5,5,-1.5,1.5]);
grid on;
%绘制DSB功率谱
subplot(313)
plot(f,psf);
xlabel('f');
ylabel('psf');
%plot(f,abs(st1));
axis([-2*fc 2*fc 0 max(psf)+0.5]);
title('DSB信号功率谱');
grid on;

仿真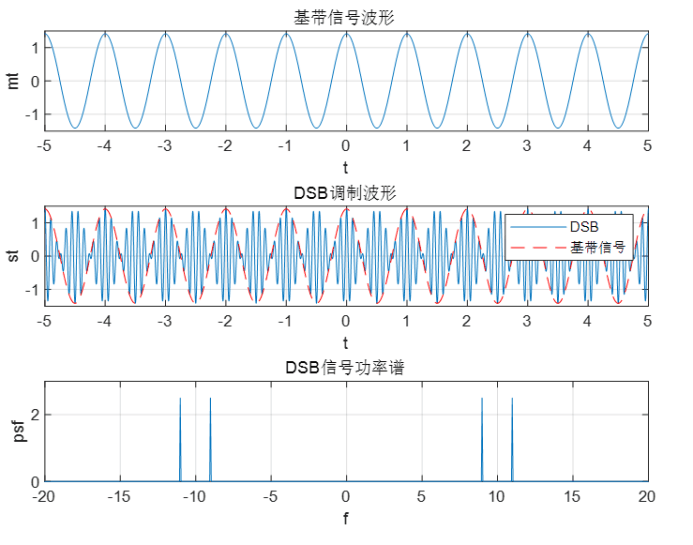

分析：
先产生一个低频的消息信号m(t)和一个高频的载波信号，用载波信号对消息信号做DSB调制，产生的第一个图像为DSB信号的时域波形，第二个图像为DSB信号的功率谱密度。可以看出，DSB调制之后，消息信号频谱被搬移到了载频附近，形成了双边谱，功率谱密度图中不包含载频频率。
2.将已调信号解调，在时域内将解调后的波形与原信号进行对比；

clc,clear,close all;
dt=0.001;
t=-10:dt:10;% 仿真时间
fm=1;%基带信号频率
fc=10;%载波频率
w_lpf = 1; % 低通滤波器截止频率（理想）
mt=sqrt(2)*cos(2*pi*fm*t);%基带信号
c=cos(2*pi*fc*t);%载波信号
st=mt.*c;%DSB
%解调
st1=st.*c;
sample = length(t);
st2 = fft(st1, sample)mple*2; % 这里要/抽样次数*2 才是最后结果
f = 1/dtmple*(0:1:sample-1);
st3 = st2.*(f<w_lpf); % 进过低通滤波
st4 = real(ifft(st3)); %解调后波形
%绘制基带信号
subplot(311)
plot(t,mt)
xlabel('t');
ylabel('mt');
%plot(t,mt,'r--')
title('基带信号波形');
axis([-5,5,-1.5,1.5]);
grid on;
%绘制DSB波形
subplot(312)
plot(t,st)
xlabel('t');
ylabel('st');
hold on;
plot(t,mt,'r--');
title('DSB调制波形');
legend('DSB信号','基带信号')
axis([-5,5,-1.5,1.5]);
grid on;
%绘制解调后信号与原信号波形对比
subplot(313)
plot(t,st4*sample);
hold on;
plot(t,mt)
xlabel('t');
ylabel('st1');
%plot(f,abs(st1));
axis([-5,5,-1.5,1.5]);
hold on;
%plot(t,mt,'r--');
title('解调后波形');
legend('解调后信号','基带信号')
grid on;

仿真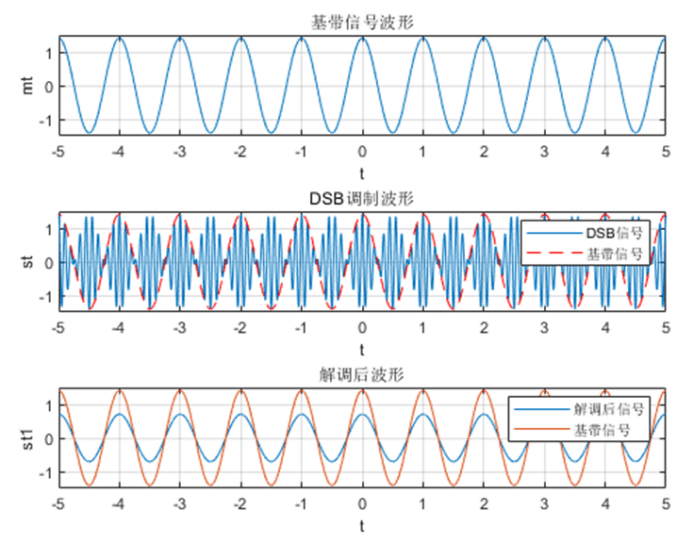

分析：
在实验1的基础上，通过相干解调法，将DSB调制之后的信号解调，并与调制前消息信号对比。可以看出，解调之后能恢复出消息信号，但是信号幅度变为原来的1/2左右，符合相关理论知识。
3.A=2的AM调制信号及其功率谱密度；

clc,clear,close all;
dt=0.001;
t=-10:dt:10;% 仿真时间
A=2;
fm=1;%基带信号频率
fc=10;%载波频率
w_lpf = 1; % 低通滤波器截止频率（理想）
w_ipf = 1; % 带通滤波器截止频率（理想）
fm = 0.3; % 带通滤波器通带
mt=sqrt(2)*cos(2*pi*fm*t);%基带信号
c=cos(2*pi*fc*t);%载波信号
st=(mt+A).*c;%AM
%解调
st1=st.*c;
sample = length(t);
st2 = fft(st1, sample)mple*2; % 这里要/抽样次数*2 才是最后结果
f = 1/dtmple*(0:1:sample-1);
st3 = st2.*(f<w_lpf); % 进过低通滤波
st4 = real(ifft(st3)); %解调后波形
%求功率谱
T=20;
df=1/T;%抽样精度
N=length(st);%确定抽样个数
f=-N/2*df:df:N/2*df-df;%功率谱范围
sf=fft(st);%傅里叶变化
sf=T/N*fftshift(sf);%将零频点移到频谱的中间
psf=(abs(sf).^2)/T;%求功率
%绘制基带信号
subplot(411)
plot(t,mt)
xlabel('t');
ylabel('mt');
%plot(t,mt,'r--')
title('基带信号波形');
axis([-5,5,-1.5,1.5]);
grid on;
%绘制AM波形
subplot(412)
plot(t,st)
xlabel('t');
ylabel('st');
hold on;
plot(t,mt+2,'r--');
title('AM调制波形');
legend('AM','基带信号')
axis([-5,5,-5,5]);
grid on;
%绘制AM功率谱
subplot(413)
plot(f,psf);
xlabel('f');
ylabel('psf');
%plot(f,abs(st1));
axis([-2*fc 2*fc 0 max(psf)]);
title('AM信号功率谱');
grid on;
%绘制解调后信号与原信号波形对比
subplot(414)
plot(t,st4*sample-2)
xlabel('t');
ylabel('st4');
%plot(f,abs(st1));
axis([-10,10,-3,3]);
hold on;
plot(t,mt,'r--');
title('解调后波形');
legend('解调后信号','基带信号')
grid on;

仿真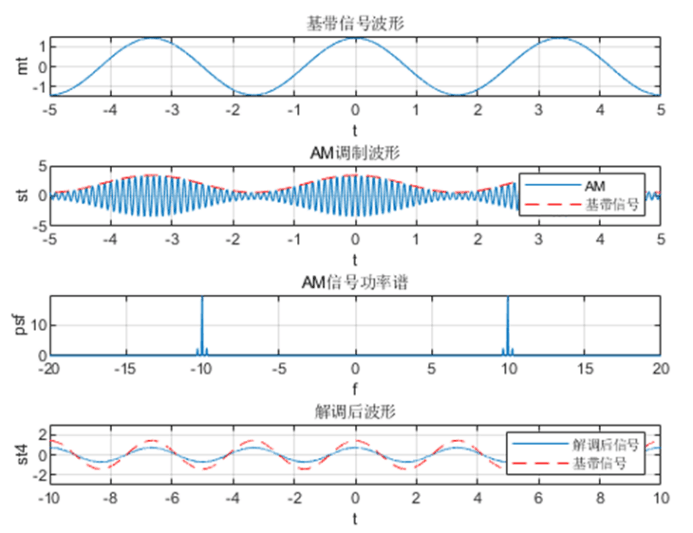

分析：
先产生一个低频的消息信号m(t)和一个高频的载波信号，用载波信号对消息信号做AM调制，产生的第一个图像为AM信号的时域波形，第二个图像为AM信号的功率谱密度。可以看出，AM调制之后，消息信号频谱被搬移到了载频附近，形成了双边谱+载波频谱。
4.SSB调制信号及其功率谱密度；

clc,clear,close all;
dt=0.001;
t=-10:dt:10;% 仿真时间
fm=1;%基带信号频率
fc=10;%载波频率
w_lpf = 1; % 低通滤波器截止频率（理想）
w_ipf = 1; % 带通滤波器截止频率（理想）
fm = 0.3; % 带通滤波器通带
mt=sqrt(2)*cos(2*pi*fm*t);%基带信号
c=cos(2*pi*fc*t);%载波信号
st=real(hilbert(mt).*exp(j*2*pi*fc*t));%SSB
%解调
st1=st.*c;
sample = length(t);
st2 = fft(st1, sample)mple*2; % 这里要/抽样次数*2 
f = 1/dtmple*(0:1:sample-1);
st3 = st2.*(f<w_lpf); % 进过低通滤波
st4 = real(ifft(st3)); %解调后波形
%求功率谱
T=20;
df=1/T;%抽样精度
N=length(st);%确定抽样个数
f=-N/2*df:df:N/2*df-df;%功率谱范围
sf=fft(st);%傅里叶变化
sf=T/N*fftshift(sf);%将零频点移到频谱的中间
psf=(abs(sf).^2)/T;%求功率
%绘制基带信号
subplot(411)
plot(t,mt)
xlabel('t');
ylabel('mt');
%plot(t,mt,'r--')
title('基带信号波形');
axis([-5,5,-2,2]);
grid on;
%绘制SSB波形
subplot(412)
plot(t,st)
xlabel('t');
ylabel('st');
hold on;
plot(t,mt,'r--');
title('SSB调制波形');
legend('SSB','基带信号')
axis([-5,5,-2,2]);
grid on;
%绘制SSB功率谱
subplot(413)
plot(f,psf);
xlabel('f');
ylabel('psf');
%plot(f,abs(st1));
axis([-2*fc 2*fc 0 max(psf)]);
title('SSB信号功率谱');
grid on;
%绘制解调后信号与原信号波形对比
subplot(414)
plot(t,st4*sample)
xlabel('t');
ylabel('st4');
%plot(f,abs(st1));
axis([-10,10,-2,2]);
hold on;
plot(t,mt,'r--');
title('解调后波形');
legend('解调后信号','基带信号')
grid on;

仿真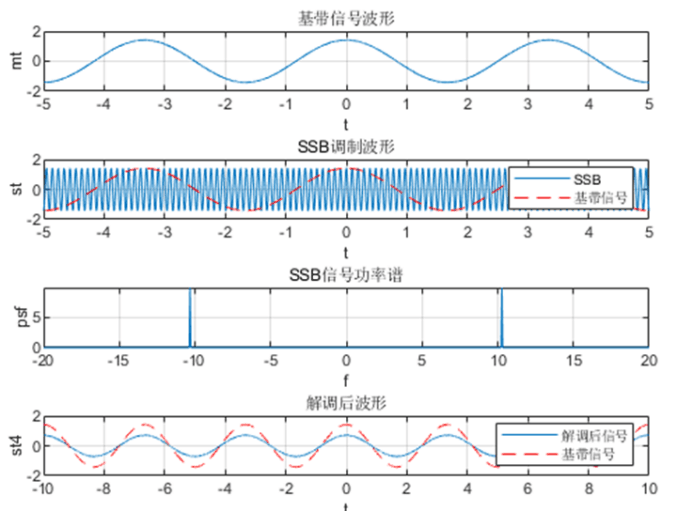

分析：
先产生一个低频的消息信号m(t)和一个高频的载波信号，用载波信号对消息信号做SSB调制，产生的第一个图像为SSB信号的时域波形，第二个图像为SSB信号的功率谱密度。可以看出，SSB调制之后，消息信号频谱被搬移到了载频附近，形成了单边谱（上边带）。
5.在信道中各自加入经过带通滤波器后的窄带高斯白噪声，功率为0.1，解调各个信号，并画出解调后的波形。

clc,clear,close all;
A=2;
dt=0.001;
t=-10:dt:10;% 仿真时间
fm=1;%基带信号频率
fc=10;%载波频率
w_lpf = 1;% 低通滤波器截止频率（理想）
w_ipf=1; % 带通滤波器截止频率（理想）
mt=sqrt(2)*cos(2*pi*fm*t);%基带信号
c=cos(2*pi*fc*t);%载波信号
%获得各种信号
st1=mt.*c;%DSB信号
st2=(mt+A).*c;%AM信号
st3= 0.5*mt.* c + 0.5*hilbert(mt).*hilbert(c); %SSB信号
%给各种信号加高斯白噪声
st11=awgn(st1,-10);%DSB信号加高斯白噪声
st22=awgn(st2,-10);%AM信号加高斯白噪声
st33=awgn(st3,-10);%SSB信号加高斯白噪声
%解调
sample = length(t);
f = 1/dtmple*(0:1:sample-1);
st11=st11.*c;%DSB信号解调
st111 = fft(st11, sample)mple*2; % 这里要/抽样次数*2 才是最后结果
st111 = st111.*(f<w_lpf); % 进过低通滤波
st1111 = real(ifft(st111)); %解调后波形
st22=st22.*c;%AM信号解调
st222 = fft(st22, sample)mple*2; %这里要/抽样次数*2 才是最后结果
st222 = st222.*((f>w_ipf-fm) - (f>w_ipf+fm) );%进过低通滤波
st2222 = real(ifft(st222)); %解调后波形
st33=st33.*c;%SSB信号解调
st333 = fft(st33, sample)mple*2; % 这里要/抽样次数*2 才是最后结果
st333 = st333.*((f>w_ipf-fm) - (f>w_ipf+fm) ); % 进过低通滤波
st3333 = real(ifft(st333)); %解调后波形
%DSB经过高斯白噪声后解调波形与原波形比较
subplot(311);
plot(t,st1111*sample);
xlabel('t');
ylabel('mt');
hold on;
plot(t,mt,'r--');
title('经过高斯白噪声后波形比较');
legend('DSB','基带信号');
axis([-5,5,-1.5,1.5]);
grid on;
%AM经过高斯白噪声后解调波形与原波形比较
subplot(312)
plot(t,st2222*sample)
xlabel('t');
ylabel('mt');
hold on;
plot(t,mt,'r--')
title('经过高斯白噪声后波形比较');
legend('AM','基带信号');
axis([-5,5,-1.5,1.5]);
grid on;
%SSB经过高斯白噪声后解调波形与原波形比较
subplot(313)
plot(t,st3333*sample)
xlabel('t');
ylabel('mt');
hold on;
plot(t,mt,'r--');
title('经过高斯白噪声后波形比较');
legend('SSB','基带信号')
axis([-5,5,-1.5,1.5]);
grid on;

仿真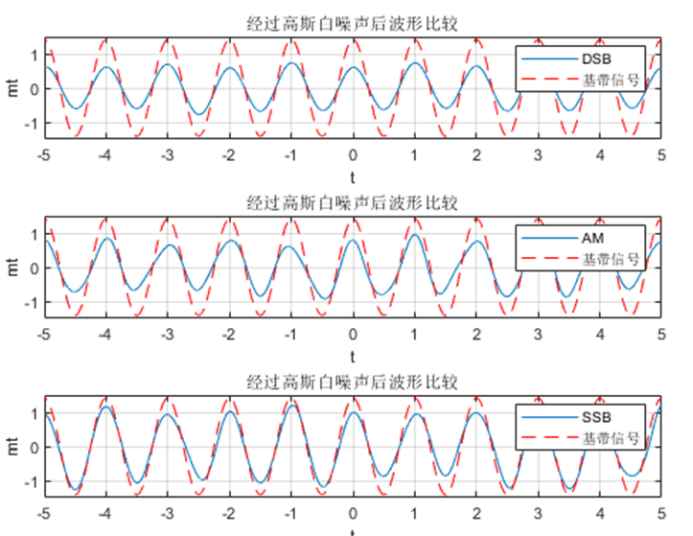

分析：
加入噪声后，时域波形明显失真，但是由于加入的噪声较小，信号仍能在解调后得到不错的恢复。

思考题

1.对三种调制信号及其功率谱密度进行比较分析；
答：（1）AM信号：ma≤1时，AM信号的包络变化与消息信号 m(t) 振幅的变化规律一致；消息信号频谱搬到了载频附近，同时具有上下边带和载频分量，带宽为基带信号带宽的两倍，特点是载波功率大，功率利用率低
（2）DSB信号：包络不再和m（t）成正比，当m(t)改变符号时载波相位反转，故不能采用包络检波，需相干解调；无载频分量，只有上边带、下边带，带宽是基带信号带宽的两倍，无载频分量，调制效率100%，功率利用率高
（3）SSB信号：包络不和 m（t）成正比，故不能采用包络检波；只包含上边带或下边带，带宽等于基带信号带宽，特点是无载频分量，调制效率100%，功率利用率高
2.在上述相干解调中，已经假设本地振荡器的相位等于载波的相位。如果它们之间存在某一个相移$\phi$，解调过程会如何改变？
答：载波同步是相干解调方式中至关重要的一个步骤，如果载波不同步，解调过程将引起严重失真，无法恢复原始波形。